こんにちは!うちやま ( @s_uchiyama_1 ) です。
今回のテーマは
指数の拡張 (1) 自然数から整数へ
です!
今回の授業内容をざっくりと理解したい人は、まずは下の動画(YouTube)をご覧ください!
気に入ったらチャンネル登録もお願いします!
授業
はじめに
今回は「指数の拡張 (1) 自然数から整数へ」について学んでいきます。
指数は中学数学で学びました。
\(2\) を \(3\) 回かけたもの、つまり
\( 2 \times 2 \times 2 \)
のことを
\(2^3\)
と表すことにして、これを「 \(2\) の \(3\) 乗」と呼びました。
このとき、右上に小さく書かれている数 ( \(3\) ) のことを「指数」といいましたね。
今までは、\(1\) 乗 , \(2\) 乗 , \(3\) 乗 , \(\cdots\) のように、指数の範囲はすべて「自然数」で考えていました。
高校数学では、指数の範囲を「整数」まで拡張して
\(0\) 乗 , \(-1\) 乗
なども計算できるようにしていきます。
ところが
\( 2^3 \) → \(2\) を \(3\) 回かける
と同じように
\( 2^0 \) → \(2\) を \(0\) 回かける(?)
\( 2^{-1} \) → \(2\) を \(−1\) 回かける(??)
と考えても、意味がわからないですね。
そこで「○回かける」という意味はいったん忘れて、数学的に矛盾がないようにこれらの値を「決めていく ( = 定義する) 」ことで、指数の範囲を自然数から整数に拡張していきます。
「数学的に矛盾がない」というのは「指数法則が成り立つ」ということです。
指数法則は中学数学で学びましたが、指数が整数に拡張されても同じ法則が成り立って欲しいと考えるのが普通ですね。
そこで、今までの指数法則がそのまま成り立つように指数を整数まで拡張していきます。
ということで今回の目標はコチラです。
指数の範囲を整数まで拡げて、\(2^0\) や \(2^{-1}\) などの値を求めることができる
それでは、始めましょう!
指数を自然数から整数に拡張する
それでは、指数の範囲を自然数から整数に拡張していきましょう。
例として、\(2^0\) や \(2^{-1}\) の値を決めることを考えてみます。
今までの規則が崩れないように…
まず、\( 2^1=2 \) , \( 2^2 = 4 \) , \( 2^3=8 \) となることは良いでしょう。このとき
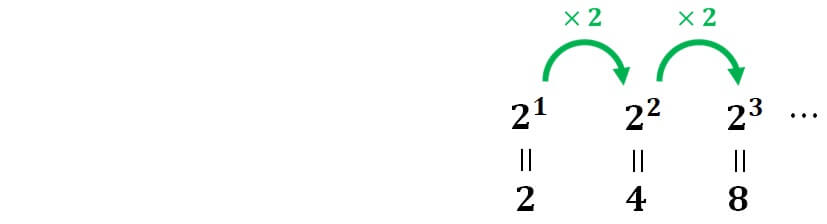
このように、値が \(2\) 倍ずつ大きくなっていくという規則に注目すると
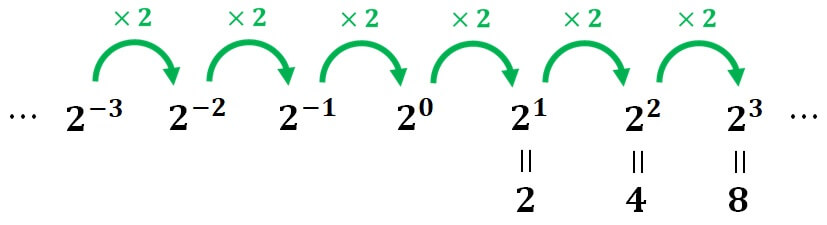
このように、その規則が崩れないように \(2^0\) や \(2^{-1} \) などの値を決めたくなるのが自然ですね。
\(2^0\) の値を決める
それではまず \(2^0\) の値を決めましょう。
\(2^0\) の値を \(2\) 倍すると \(2^1 (=2) \) になればよいことから
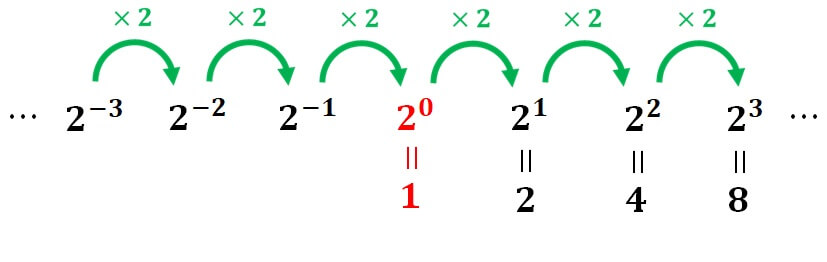
このように \(2^0=1\) と決めればよさそうです。
\(2^{-1}\) , \(2^{-2}\) , \(2^{-3}\), \(\cdots\) の値を決める
さらに、\( 2^{-1}\) , \(2^{-2}\) , \( 2^{-3}\) , \( \cdots \) も同じように考えれば
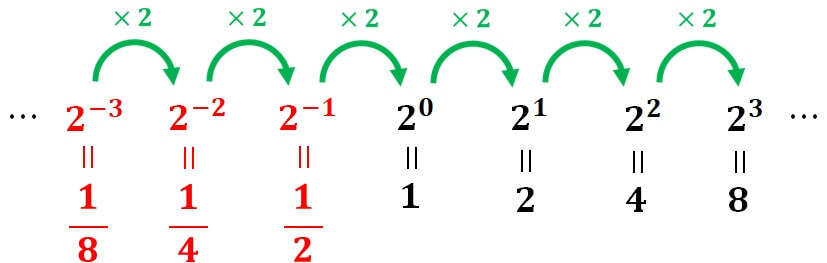
このように決めればよさそうです。
ここで
\( \displaystyle 2^{-1}=\frac{1}{~2~}=\frac{1}{~2^1~} \)
\( \displaystyle 2^{-2}=\frac{1}{~4~}=\frac{1}{~2^2~} \)
\( \displaystyle 2^{-3}=\frac{1}{~8~}=\frac{1}{~2^3~} \)
と表すことができるので、\(n\) を自然数として
\( \displaystyle 2^{-n} =\frac{1}{~2^n~} \)
と決めればよいことがわかります。
以上まとめれば
\( 2^{0} = 1 \)
\( \displaystyle 2^{-n} =\frac{1}{~2^n~} \) ( \(n\) は自然数)
と決めることで、これまでの規則を崩さないように指数が \( 0 \) や 負の整数の場合も考えることができるようになりました。
まとめ
今の話は、\( 0 \) 以外の数 \( a \) に対しても同じように考えれば
\( a^0 = 1\)
\( \displaystyle a^{-n} = \frac{1}{a^n} \) ( \(n\) は自然数)
と決めればよいことがわかります。
ということで、指数を整数まで拡張したときは、次のように計算すればよいことになります。
指数の拡張 (自然数から整数へ)
\( a^0 = 1\) , \( \displaystyle a^{-n} = \frac{1}{~a^n~} \)
ただし、\( a \ne 0 \) , \( n \) は自然数。

授業はここまでです!
それでは、例題を解いていきましょう!
例題
次の値を求めよ。
(1) \( 4^0 \) (2) \( 3^{-2}\) (3) \( (-5)^{-3} \) (4) \( 0.2^{-2}\)
解答
(1)
\( 4^0 = 1 \) \(\cdots\) (答)
(2)
\( \displaystyle 3^{-2} = \frac{1}{~3^2~} = \frac{1}{~9~} \) \(\cdots\) (答)
(3)
\( \displaystyle (-5)^{-3} = \frac{1}{~(-5)^3~} =- \frac{1}{~125~} \) \(\cdots\) (答)
(4)
\( \displaystyle 0.2^{-2} = \frac{1}{~0.2^2~} = \frac{1}{~0.04~} = \frac{~100~}{4} = 25 \) \(\cdots\) (答)
解説
◇ 指数が \(0\) や負の数の場合は
\( a^0 = 1\) , \( \displaystyle a^{-n} = \frac{1}{~a^n~} \)
を使って計算していきます。
計算ミスをしないように \(1\) つずつ丁寧に計算していきましょう。もちろん、慣れてきたら省略して書けるようになりましょう。
◇ (4) については別解を紹介します。
まず、次の性質が成り立ちます。
分数の \(-n\) 乗は逆数の \(n\) 乗
\( \displaystyle \left( \frac{a}{~b~} \right)^{-n} = \left( \frac{b}{~a~} \right)^n \)
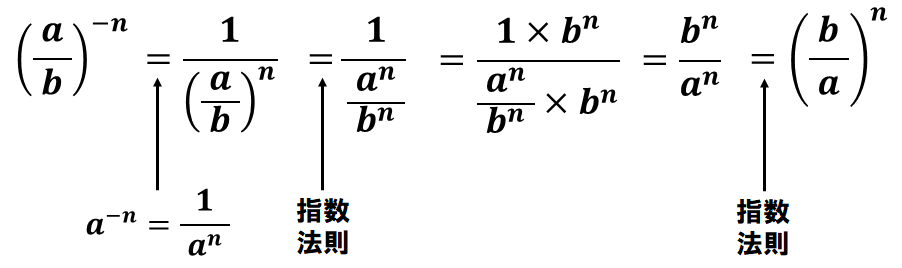
結構使える性質ですので、ぜひ頭に入れてほしいと思います。
「分数の \(-n\) 乗は逆数の \(n\) 乗」と覚えておくとよいでしょう。
この性質を使うと、次のように解くこともできます。
(4) (別解)
\( \displaystyle 0.2^{-2} \)
\( \displaystyle = \left( \frac{1}{~5~} \right)^{-2} \)
\( \displaystyle = \left( \frac{5}{~1~} \right)^{2} \)
\(= 5^2 \)
\(= 25 \) \(\cdots\) (答)

今回はここまで!
おつかれさまでした!



コメント