こんにちは!うちやま ( @s_uchiyama_1 ) です。
今回のテーマは
指数関数のグラフ
です!
今回の授業内容をざっくりと理解したい人は、まずは下の動画(YouTube)をご覧ください!
気に入ったらチャンネル登録もお願いします!
授業
はじめに
今回は「指数関数 \( y=a^x \) のグラフ」について学んでいきます。
\( y=a^x \) という形の関数を、指数関数といいます。
まず、指数関数のグラフの形を学びます。
指数関数のグラフは、\(y=a^x\) の \(a\) の値によって大きく \(2\) つに分かれます。
次に、グラフの \(3\) つの特徴を学びます。
指数関数のグラフを描くときにはこの \(3\) つの特徴に気を付けながら描きましょう。
ということで今回の目標はコチラです。
指数関数のグラフの形と特徴を学ぶ
それでは、始めましょう!
指数関数とは?
\( y=a^x \) という形の関数を指数関数といいます。
このときの \(a\) を底 (てい)といい、底には
\( a > 0 \) かつ \( a \ne 1 \)
という条件がつきます。
また、\(x\) にはどんな実数でも代入することができますので、指数関数 \( y=a^x \) の定義域は実数全体です。
指数関数のグラフの形
それでは、指数関数 \( y=a^x \) のグラフを描いていきましょう。
まずは \(2\) つの例を一気に見て、その後にグラフの特徴などをまとめていきます。
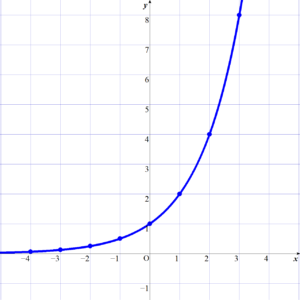
[例1] \( y=2^x \) のグラフ
それぞれの \(x\) の値に対応する \(y\) の値を求めると、次のようになります。

(値の求め方が分からない場合は「指数の拡張 (1) 」を参照してください。)
そして、これらを座標とする点をとって曲線で結ぶと下図のようになります。
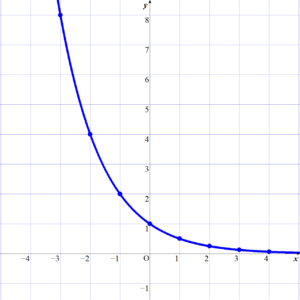
[例2] \( \displaystyle y=\left(\frac{1}{2} \right)^x \) のグラフ
それぞれの \(x\) の値に対応する \(y\) の値を求めると、次のようになります。

そして、これらを座標とする点をとって曲線で結ぶと下図のようになります。
指数関数のグラフの特徴
さて、一気に \(2\) つのグラフを見てもらいました。
ここで、指数関数のグラフの特徴をまとめていきましょう。
特徴1:グラフは単調増加または単調減少な曲線
[例1] と [例2] を見比べると、指数関数のグラフは底の値によって形が変わることがわかりますね。
具体的には
◇ \( a>1 \)のとき、グラフは単調増加 ( [例1] )
◇ \( 0<a<1 \) のとき、グラフは単調減少 ( [例2] )
となります。
ここで出てきた「単調増加」「単調減少」というのは、ただ「増える」「減る」ととらえておけば今の段階では十分です。
特徴2:\(y\) 切片は \(1\)
\(y\) 切片は \( y=a^x \) に \( x=0 \) を代入したときの値です。
よって、\( y=a^0=1 \) となりますね。
特徴3:\( y \) の値は常にプラスとなる ( \(x\) 軸には触れない )
グラフを描く前に作った表を見れば明らかですが、\(y\) の値は常にプラスとなります。つまり、グラフは \(x\) 軸には絶対に触れません。
このときの \(x\) 軸のような直線を漸近線といいます。
まとめ
以上が指数関数 \( y=a^x \) のグラフの特徴です。
ただし、グラフを平行移動・対称移動・拡大縮小すると、関数の式が変わるためこれらの特徴が成り立たない場合もがありますので注意してください。
指数関数 \( y = a^x \) のグラフ
\( a>1 \) のとき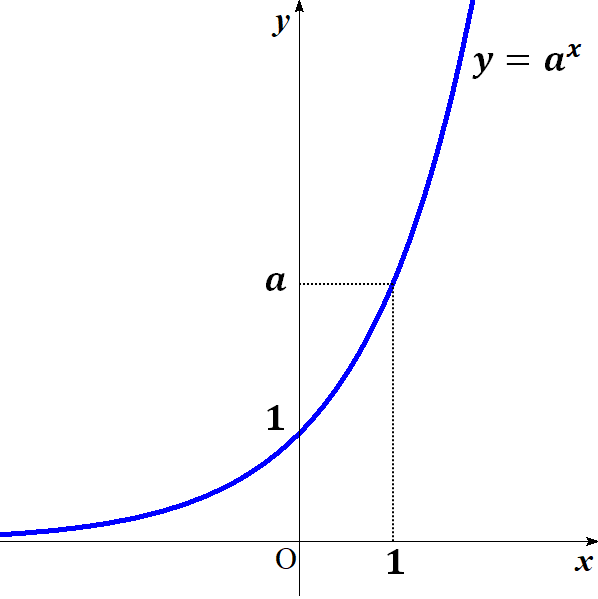
\( 0<a<1 \) のとき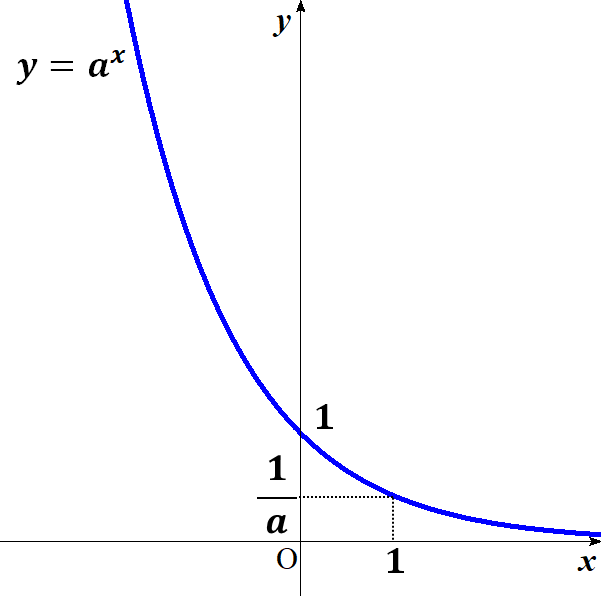
グラフの特徴
◇ \(a>1\) のとき、単調増加
\(0<a<1\) のとき、単調減少
◇ \(y\) 切片は \(1\)
◇ \( y \) の値は常にプラスとなる ( \(x\) 軸が漸近線 )

授業はここまでです!
それでは、例題を解いていきましょう!
例題
次の関数のグラフをかけ。
(1) \( y = 3^x \)
(2) \( y = -3^x \)
(3) \( y = 3^{-x} \)
(4) \( y = -3^{-x} \)
(5) \( y = 3^{x+1} \)
解答
(1)
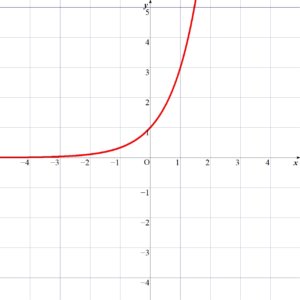
(2)
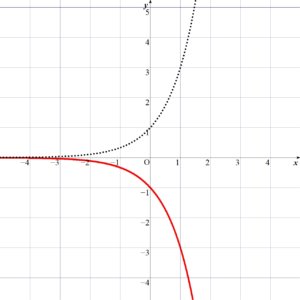
\( y = -3^x \) のグラフは、\( y = 3^x \) のグラフを \(x\) 軸に関して対称移動したものである。
( 点線は (1) \( y=3^x\) のグラフ )
(3)
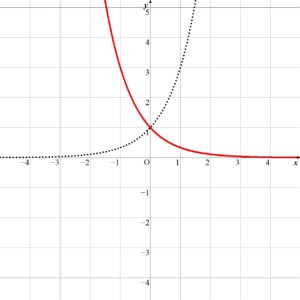
\( y = 3^{-x} \) のグラフは、\( y = 3^x \) のグラフを \(y\) 軸に関して対称移動したものである。
( 点線は (1) \( y=3^x\) のグラフ )
(4)
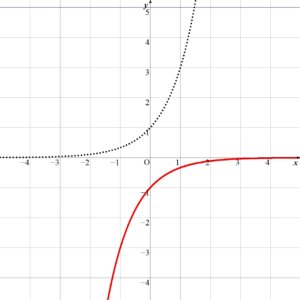
\( y = -3^{-x} \) のグラフは、\( y = 3^x \) のグラフを 原点に関して対称移動したものである。
( 点線は (1) \( y=3^x\) のグラフ )
(5)
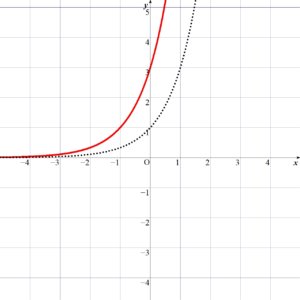
\( y = 3^{x+1} \) のグラフは、\( y = 3^x \) のグラフを \(x\) 軸方向に \(-1\) だけ平行移動したものである。
( 点線は (1) \( y=3^x\) のグラフ )
解説
◇ (2) ~ (5) については、(1) \( y=3^x \) のグラフとの位置関係に注目しましょう。
◇ \(2\) 次関数で学習済みですが
グラフの平行移動
関数 \( y=f(x) \) のグラフを
\(x\) 軸方向に \(p\)
\(y\) 軸方向に \(q\)
だけ平行移動したグラフの式は
\( y-q = f(x-p) \)
グラフの対称移動
関数 \( y=f(x) \) のグラフを
◇ \(x\) 軸に関して対称移動したグラフの式は
\( -y = f(x) \)
◇ \(y\) 軸に関して対称移動したグラフの式は
\( y = f(-x) \)
◇ 原点に関して対称移動したグラフの式は
\( -y = f(-x) \)
を利用します。

今回はここまで!
おつかれさまでした!



コメント